
II- Étude de fractales naturelles
a) La fougère

La fougère est très certainement la fractale naturelle la plus évidente. En effet, dès le premier abord, l'on s'aperçoit aisément de l'auto-similarité de la fougère. Tout le monde s'est déjà interrogé à ce sujet.
Si l'on observe une grande feuille, l'on peut alors voir une multitude de répliques de cette dernière dessus. En observant une réplique, l'on peut voir une multitude de répliques de cette même réplique. En observant une réplique de cette réplique, l'on peut voir une réplique de cette réplique de la première réplique. En observant la réplique de la réplique de la réplique, l'on se rend compte que... une aspirine ne serait pas de refus...
Plutôt que de gâcher de la place en paroles inutiles et incompréhensibles, observons.

S'étant intéressé aux fractales naturelles en général et tout particulièrement à la fougère, le mathématicien Michael Barnsley est parvenu à établir un modèle de fougère fractale grâce à un IFS (iterated function system), baptisée fougère de Barnsley. Considérer la fougère comme un arbre à trois branches, et de là la construire par itérations a été la clef de sa réussite. Toutefois, il a du utiliser un moyen détourné afin de pouvoir obtenir une fougère réaliste sur un ordinateur de puissance normale. Mais nous laisserons l'aspect technique, par ailleurs extrêmement bien expliqué sur un site dont nous donnons les références à la fin du TPE, pour nous intéresser à ce que cela implique. Observons en premier lieu la ressemblance frappante entre fougère naturelle et fougère de Barnsley.


Il semble donc que le modèle construit grâce à la géométrie fractale colle bien mieux à la réalité que tous les modèles euclidiens que nous pourrions inventer...
b) Un arbre: le poirier

Pourquoi le poirier? Ben, pourquoi pas. Certes, quasiment tous les arbres auraient pu remplacer le poirier. Certes. Mais, les poires sont si bonnes. Voici l'explication. Bref. Passons.
Nous étudions donc le poirier, alias pirus communis.
Schématisons dans un premier lieu la croissance (bien évidemment sans l'intervention humaine) du poirier.
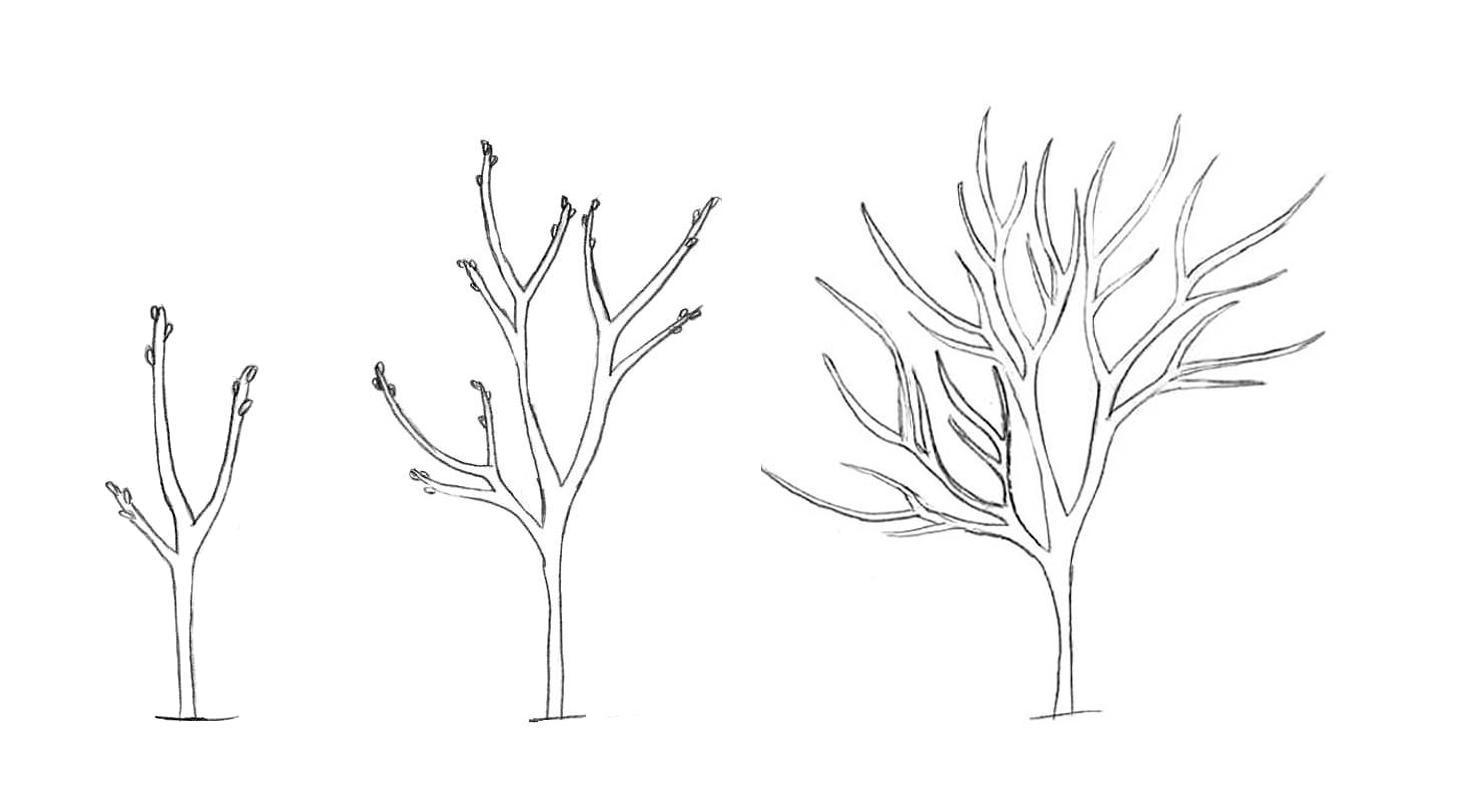
Nous avons fait ces schémas en utilisant la méthode fractale, et donc en itérant la forme du jeune poirier sur chacune de ses nouvelles branches. Le modèle semble réaliste.
Remarque: L'environnement fera bien entendu varier ce modèle que nous présentons, mais admettons qu'il s'agisse toutefois d'une sorte de matrice de base de la croissance du poirier.
Mais comment se fait-il que les branches reprennent l'allure générale qu'avait le poirier? Une réponse simple peut être apportée. les hormones de croissance sont sécrétées à l'extrémité de chaque branche, et donc pour une branche ou pour l'autre, ou même pour le tronc du tout jeune poirier, la quantité de ces hormones est répartie de la même façon. Or, la pousse des nouvelles branches est déterminée par la quantité d'hormones reçue. Ainsi, chaque nouvelle branche prend la forme de celle dont elle est issue. Le même modèle est donc réitéré à différentes échelles.
D'où nous pouvons déduire que le poirier, ainsi que beaucoup d'arbres, croît sur un modèle fractal.
c) Le modèle fractal: une optimisation des ressources.
Reste une question: POURQUOI? Pourquoi la fougère est elle une fractale? Pourquoi le poirier est il une fractale? Quel intérêt trouve la plante à croître selon un modèle fractal?
Pour comprendre, revenons aux caractéristiques mathématiques de celles-ci.
Une fractale ayant une dimension entre 1 et 2 a une surface finie et un périmètre 'infini. Une fractale ayant une dimension entre 2 et 3 a un un volume fini et une surface infinie.
Les plantes étant pour la plupart des formes en 3 dimensions, et étant des fractales naturelles, et donc imparfaites, elles ont donc un volume fini et une surface approchant de l'infini.
Quel est l'intérêt? Simple. Une plante d'un certain volume, occupant donc un certain espace, peut avoir une surface de contact entre racine et terre (pour puiser eau et sels minéraux) et entre feuilles et air (respiration, photosynthèse) optimale. Là est le pourquoi du comment.
Une plante peut, toute poésie mise à part, être comparée à une machine. Le mot essentiel est donc optimisation. Et cette optimisation est permise grâce aux fractales.
ouf.