
PARTIE1: ÉTUDE MATHÉMATIQUE DES FRACTALES
A-Première approche des fractales.
I-Définition rapide et exemples
Pour mieux comprendre, considérons dans un premier lieu les fractales comme des formes géométriques obtenues par fragmentation régulière à l’infini d’une figure donnée. Elles sont construites de sorte que si l'on zoom 1 fois,2 fois ou même 100 fois sur une partie de fractales on retrouvera le motif de la figure initiale, c'est ce que l'on appelle l'auto-similarité.
Il existe cependant de nombreuses autres façons d'aborder les fractales, notamment par leur « périmètre infini définissant une surface finie » , ou encore leur incapacité d'être dérivées (en aucun point d'une fractale ne peut être tracée de tangente). Cependant, selon les mathématiciens les ayant définies, une seule définition est réellement valable: « un objet peut être qualifié de fractal uniquement si sa dimension de Hausdorff est strictement supérieure à sa dimension topologique » . Sans exemples appropriés, cette définition peut paraître totalement indigeste pour quelqu'un n'ayant pas de connaissance en la matière. Observons donc ces courbes fractales:
1_la poussière de Cantor:

2_la courbe de Peano:
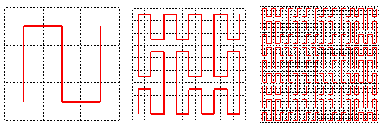
3_le triangle de Sierpinski

4_l'éponge de Sierpinski

Il paraît clair que ces fractales n'ont pas la même dimension. Et il apparaît également que trouver cette dimension s'avère difficile... En effet, quelle est la dimension d'une courbe qui occupe presque ou totalement une surface? Pour répondre à la question, Felix Hausdorff a proposé une solution: la dimension d'une fractale peut (c'est quasiment toujours le cas) ne pas être entière. Elle est alors nommée « dimension de Hausdorff », et calculée grâce à l'usage de logarithmes. Cette dimension de Hausdorff est la dimension de la fractale, comme évoqué plus haut. Elle peut ne pas être entière, et c'est d'ailleurs le cas chez la plupart des fractales. Par exemple, le flocon de Von Koch que nous étudierons plus en détail par la suite a une dimension de Hausdorff avoisinant 1,28.
La poussière de Cantor n'est ni une courbe, ni un ensemble de points. On la situerait plutôt entre les deux. On estimerait donc sa dimension de Hausdorff se trouve donc entre 0 (dimension d'un point) et 1 (dimension d'une courbe). Et l'on aurait raison, sa dimension de Hausdorff est environ égale à 0,64
Le triangle de Sierpinski, quant à lui, est entre courbe et surface. Sa dimension de Hausdorff est donc entre 1 (dimension d'une courbe) et 2 (dimension d'une surface).
La courbe de Peano est une courbe, sa dimension euclidienne devrait donc être de 1. Cependant, en théorie, après un nombre infini d'itérations, il paraît clair qu'elle remplit le plan. Sa réelle dimension, sa dimension de Hausdorff, est donc de 2.
L'éponge de Sierpinski est entre volume et surface, sa dimension est entre 2 (dimension d'une surface) et 3 (dimension d'un volume).
Vous voici imbattable sur les notions de dimensions fractales.